Review of A. Cabello et al, Thermodynamical cost of some interpretations of quantum theory, (2016)
Summary:
This paper examines the distinguishability of various interpretations of quantum mechanics by establishing two classes of theories. A type I theory is one for which the probabilities of measurement outcomes are determined solely by intrinsic properties of the observed system for which the probabilities are observer independent. A type II theory is one for which the probabilities come about from the correlation or relation between observer and system. The authors introduce the following assumptions, “(i) The choice of which measurement is performed on a system under observation can be made randomly and independently of the quantum system, (ii) the system has limited memory, and (iii) Landauer’s erasure principle holds.” The authors claim that type I theories are incompatible with assumptions (i)-(iii).
In standard quantum theory, a system in an initial state ![]() that is measured by a rank 1 projector
that is measured by a rank 1 projector ![]() is changed to
is changed to ![]() upon successful measurement. That is, the initial system state
upon successful measurement. That is, the initial system state ![]() is lost or erased. Hence measurement theories need to address how this occurs if they are to produce results that agree with standard quantum theory. It is claimed by Cabello et al that for type I theories with finite system memory, eventually it will need to be overwritten. And because the system is overwritten, a given amount of dissipation needs to occur due to Landauer’s principle.
is lost or erased. Hence measurement theories need to address how this occurs if they are to produce results that agree with standard quantum theory. It is claimed by Cabello et al that for type I theories with finite system memory, eventually it will need to be overwritten. And because the system is overwritten, a given amount of dissipation needs to occur due to Landauer’s principle.
Comments:
- That one can potentially distinguish between different interpretations is interesting. In references [1,2] models are proposed which are claimed to be counterexamples to the Cabello et al result. The authors respond in [3] that the models in [1,2] that purport to be a type I theory are in fact not type I theories
- The authors consider an electron in the measurement process. However, suppose a photon is measured and carries the information for which the probabilities of measurement outcomes are determined. A photon may be annihilated in the process of measurement, and absorbed in the measurement device. No additional information need be written, nor can be written onto a photon that is annihilated after measurement. Hence if one were to study the process of photon measurement, it would seem that this theory would require further extension
- Furthermore, in the measurement of an electron (or other particle with mass) we expect that the electron and the measurement device must interact in order for measurement to occur. When two such systems are strongly interacting, they will generally exchange energy, although there are a few special exceptions. However, aside from the special exceptions, energy that dissipated from the system could be replaced by the measurement device. Hence it would seem to make more sense that the measurement device plus electron dissipate energy. However, the authors state:
Therefore, whenever the temperature is not zero, assumption (iii) implies that the system should dissipate at least an amount of heat proportional to the information erased.
We don’t see why the “system” should dissipate heat and not include the device, particularly when the device and system are strongly interacting. The argument that is given for which Type I theories are invalid under the assumptions (i)-(iii) appears to rely on the potential of large energy release from a finite energy system. That is, it is stated:
Therefore, when the temperature of the system is not zero, the lower bound of the heat dissipated by the system from Landauer’s principle tends to infinity at least linearly with n
Considering the effect of Landauer’s principle separately on the measurement device is not the same as understanding it for the interacting system-device including the exchange of energy between them. Cabello et al cite reference [5] as theoretically justifying Landauer’s principle for quantum systems and the analysis in [5] obtained the heat dissipated for a quantum system initially coupled to a thermal reservoir and then jointly undergoing unitary evolution. Moreover, from [4] it is also stated that
Landauer’s principle, often regarded as the basic principle of the thermodynamics of information processing, holds that any logically irreversible manipulation of information, such as the erasure of a bit or the merging of two computation paths, must be accompanied by a corresponding entropy increase in non-information-bearing degrees of freedom of the information-processing apparatus or its environment.
The resulting heat generally needs to be expressed in terms of not only the system entropy as in the classical Landauer principle but also the mutual information between system and reservoir and the free energy increase in the reservoir. Thus, quantum systems require a more general Landauer principle in which the states of both the system and reservoir vary during the erasure process and this has been verified in experimental atomic systems [6]. To properly consider the influence of Landauer’s principle on quantum measurement, the above would have to be included in a study of an interacting system-measurement-device in which energy can be exchanged between them.
That is, there is no requirement that the entropy increase occur within only the system between the time of initial interaction with the measurement device and the time after a measurement has been recorded. If energy can flow from the device to the system or visa-versa in the process of measurement interaction, it would seem to weaken or invalidate the conclusions reached in this paper. - The standard setup of the quantum measurement problem that is often considered is the following, Suppose an apparatus initially in state
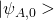 will evolve to final state
will evolve to final state 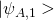 when the system is applied initially in state
when the system is applied initially in state 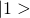 , and whereby the apparatus will evolve to
, and whereby the apparatus will evolve to 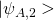 when the system is initially in state
when the system is initially in state 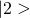 . Now if the system is initially in the state
. Now if the system is initially in the state 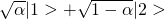 , unitary evolution implies the final state to be
, unitary evolution implies the final state to be 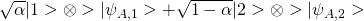 whereas the measurement postulate implies the final state is
whereas the measurement postulate implies the final state is  with probability
with probability 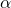 and
and  with probability
with probability 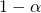 . In the latter case the system on-average is mathematically similar to a mixed state for local computations (but not necessarily non-local computations).
. In the latter case the system on-average is mathematically similar to a mixed state for local computations (but not necessarily non-local computations).
Now, in the quantum measurement problem setup, an initially pure system state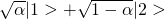 evolves on average to a mixed system state. As the entropy of the initial pure state is zero, the entropy decrease of the system in Landauer’s theorem (defined as the initial entropy of the system minus the final entropy) will be negative. It is stated in [5] that their results also apply to the case when entropy increases in the system, for which it is possible for heat to flow from the reservoir into the system.
evolves on average to a mixed system state. As the entropy of the initial pure state is zero, the entropy decrease of the system in Landauer’s theorem (defined as the initial entropy of the system minus the final entropy) will be negative. It is stated in [5] that their results also apply to the case when entropy increases in the system, for which it is possible for heat to flow from the reservoir into the system.
In Cabello et al, the authors compute the information that is erased in their Equation (4) by assuming a fixed final state for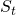 and then sum over the possibilities of states at
and then sum over the possibilities of states at 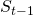 that could have given rise to
that could have given rise to 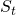 . In this sense the authors are going from a mixed state to a pure state. On the other hand the standard measurement problem starts with a known pure superposition initial state and evolves to on-average a mixed state indicative of the multiple possible measurement results. It appears that the Cabello et al approach is reversed as compared to the standard setup in the quantum measurement problem. And in the case that the initial state superposition is pure, the von Neumann entropy of the initial state is zero.
. In this sense the authors are going from a mixed state to a pure state. On the other hand the standard measurement problem starts with a known pure superposition initial state and evolves to on-average a mixed state indicative of the multiple possible measurement results. It appears that the Cabello et al approach is reversed as compared to the standard setup in the quantum measurement problem. And in the case that the initial state superposition is pure, the von Neumann entropy of the initial state is zero. - Cabello’s justification for applying Landauer to quantum systems is Reeb et al [5]. However, the Reeb et al result reduces to Landauer only for infinite reservoirs. Yan et al’s [6] experimental verification of the Reeb et al result also used the vibrational modes of the Ca+ ion as the reservoir and was finite. Justification of an infinite reservoir ought to be provided.
- Overall even with these flaws, the paper is interesting, but we feel that a number of issues still need to be addressed.
Minor issues:
The collapse models of GRW are not simply interpretations of quantum mechanics, as they introduce new physics.
[1] C. E. A. Prunkl, C. Timpson, On the thermodynamical cost of some interpretations of quantum theory, Stud. Hist. Philos. Sci. Part B: Stud. Hist. Philos. Mod. Phys. 63, 114 (2018).
[2] E. Davidsson, Landauer’s principle — Its classical conception and extension to quantum mechanics, Masters thesis, Stockholm University, Stockholm (2018).
[3] A. Cabello, M. Gu, O. Gühne, J. A. Larsson, K. Wiesner, The thermodynamical cost of some interpretations of quantum theory. Reply to Prunkl and Timpson, and Davidsson. Quant-ph/1901.00925v1 (2019).
[4] C. Bennett, Notes on Landauer’s principle, reversible computation, and Maxwell’s Demon, Studies in History and Philosophy of Modern Physics 34 (2003) 501–510
[5] D. Reeb, M.M. Wolf, An improved Landauer principle with finite-size corrections, New Journal of Physics 16, 103011 (2014).
[6] L.L.Yan, T.P. Xiong, K. Rehan, F. Zhou, D.F. Liang, L. Chen, J.Q. Zhang, W.L. Yang, Z.H. Ma, M. Feng, Single-Atom Demonstration of the Quantum Landauer Principle, Phys. Rev. Lett. 120, 210601 (2018).

Very nice post. I just stumbled upon your blog and wanted to say that I have truly enjoyed browsing your blog posts. In any case I’ll be subscribing to your feed and I hope you write again very soon!
Some really superb blog posts on this internet site , thankyou for contribution.