admin

Review of S. Donadi and S. Hossenfelder, Toy model for local and deterministic wave-function collapse PHYSICAL REVIEW A 106, 022212 (2022)

Summary:

The authors present a model for wave-function collapse based on the system-measurement device evolving as a closed system via non-unitary evolution of the Lindblad form depending on the value of local hidden variables.  The hidden variables contain information of both measurement settings in a Bell experiment. Hence the model violates statistical independence of the hidden variables and the measurement settings which was an assumption of Bell.  The authors use this model to develop a local deterministic toy model that makes the same predictions as the collapse postulate.  The model is based around a Lindblad equation, but with a variation.  Normally the Lindblad equation has a number of matrices L_{12} which are utilized in a summation of terms. However, in this case the matrices vary in time and converge toward a single term that, summed over the matrices that are generally applied as a sum in the Lindblad equation, is instead applied directly.

The specific matrices utilized in the Lindblad equation converge to either L_{12}=|\chi_{1}><\chi_{2}| or L_{12}=|\chi_{2}><\chi_{1}| and are dependent on the hidden variables. Hence an initially mixed density matrix can either approach \chi_{1} or \chi_{2} for N=2 depending on the choice of the hidden parameters. The evolution is not stochastic but deterministic in this case and does not occur instantaneously, but over a finite time. We will refer to this as a modified Lindblad equation. The authors later extend this to N>2, and consider issues of no-signaling and the requirement of statistical independence proposed by Bell later in the paper.

Remarks:

  1. The model that the authors have put forward based on locality, determinism, and hidden variables seems somewhat similar to a model based on non-locality and Born’s non-determinism. That is, consider the following model. Two entangled qubit systems head in opposite directions toward two detectors. Each local detector-system density unitarily interacts with an environment that will be represented by interaction with an ancilla.  It can be seen that according to Preskill [1, p. 37]  the same form of Lindblad equation results for the system-detector but all the terms are necessarily present in the summation as no measurement has yet been made.  Now suppose after a short interaction time 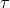\tau between each system and local ancilla we non-unitarily measure the environmental ancilla in a basis which also projects the detector-system to a pointer state.  Let us assume the result is non-deterministic. Then, this can be repeated, i.e. another short interaction time followed by a measurement.  Note that each projection of the environment will locally affect the detector that it is interacting with but also non-locally effect the second qubit. The question is how does this non-deterministic and non-local model differ in its predictions from the deterministic and local model proposed by the authors?   It would be of interest to determine this to see if such superdeterministic, local models have different signatures and can potentially be distinguished from non-deterministic, nonlocal models.
  2. Note that if an environment unitarily interacts with a detector-system as above, one might also expect that the entanglement between the two distant detector-systems decreases.  Prediction of the sudden-death of entanglement was made in [2] and a review appears in [3].  The use of a unitary bath coupling followed by projection of the bath as in 1. above might serve as a platform for further study as to if and when the detectors of the two systems eventually do not show the correct or expected Bell correlation due to entanglement.  One might consider employing a second purely unitary interaction between detector-system with a different coupling than with the first coupling which is non-unitary. By varying the two couplings and the time of interaction 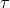\tau before non-unitary measurement of the first ancilla, one would expect to find different types of both the first order measurement time of each qubit as well as the second order effects on the entanglement. These might be used to see if there is a decoherence effect that is non-unitary versus unitary decoherence effects, and/or to rule out one or the other type of decoherence.

Strengths:

  1. The authors understand correctly from a separate paper [4] that unitary evolution will not suffice to explain the results of measurement and in this paper, they propose a non-unitary solution.
  2. The authors propose that the detector-system evolves via a modified Lindblad equation which is positive and linear in density operator.
  3. As the authors note, this has the advantage of obeying causality constraints of no-signaling.

Weaknesses:

  1. The method proposed in this experiment does not appear to make much if any progress on the main issue regarding the measurement problem that these authors proposed in their paper [4] and we also similarly proposed in our book [5]. That is, determining the specific conditions for which measurement or non-unitary evolution occurs.  Note that one would be wrong to blindly apply non-linear evolution to an electron evolving in free-space.  On the other hand, it is expected that there are conditions for which non-unitary evolution exists.  Determining these conditions is the primary requirement for a solution to the quantum measurement problem.  More work is needed along these lines.
  2. The authors claim that:

The model further violates energy conservation. Again, this is because it stands in for an effective description that, among other things, does not take into account the recoil (and resulting entanglement with) parts of the experimental equipment.

That is not obvious to us. Recoil has specific requirements and one cannot utilize an arbitrary recoil to balance energy.  Consider a measuring device that has some 1) initial velocity, 2) initial mass, 3) final mass, 4) final velocity, and as well as the system to be measured which consists of a photon that has an 5) energy and is absorbed by the device upon measurement.  It can be shown by conservation of energy and momentum arguments, that any three of these variables determines the remaining two.  Neither five nor four of these variables can be set independently. So, there is clearly a constraint when applying recoil arguments and it appears to us that one needs to demonstrate with their particular Lindblad model that recoil will actually work to conserve energy and momentum.  That is, one cannot simply state this and expect it will always work for arbitrary parameters and Lindblad operators.  And if one subsequently performs an experiment with known values of initial and final detector velocities and masses that measure a photon of a known energy, then if one is able to estimate the Lindblad operators for a particular experiment that would fit this model assuming determinism and locality, one should be able to determine if recoil is sufficient to account for energy and momentum conservation.

The authors appear to be of the opinion that not meeting the statistical independence requirement of Bell is not really much of a problem. We disagree.  However, our disagreement is not at this time something that can be strictly ruled out at this time, so we agree that these authors should be given a chance to propose their theory and have it tested if possible. 

Now, the experimenter’s ability to change a setting independent of the past is an assumption based on the free-will of the experimenter.  Interestingly the discussion of free-will doesn’t appear in the journal paper, which is odd because it is clearly central to the entire issue.  The second author has claimed that free-will doesn’t exist [6] :

Now you all know that I think free will is logically incoherent nonsense.

And further claims:

Spooky action at a distance doesn’t make any difference for free will because the indeterministic processes in quantum mechanics are not influenced by anything, so they are not influenced by your “free will,” whatever that may be.

Emotions aside on this issue, a purely logical error is being made by applying an inductive argument to reach a conclusion to a problem which we are fairly certain necessitates a deductive approach: the conclusion that free-will doesn’t exist.  Hossenfelder believes that the conclusion follows because the current theory based on either the projection postulate or Schrödinger’s equation appears insufficient to describe free-will. Such a conclusion is based on the current theory and by definition is therefore made on the basis of inductive reasoning.  Yet the authors in a separate paper [4] have already concluded that the current theory is likely incomplete, which we agree with.  Hence, the non-existence of free-will cannot logically be concluded from a deductive argument at present, because it is agreed that the current theory is incomplete. Good try, but Sorry Charlie.

Conclusions:

The authors noted in their introduction that:

A century ago one might have hoped that quantum mechanics would one day be replaced by a theory compatible with the deterministic and local prequantum ontology.

They further note that nearly all current theories that account for measurement are fundamentally nondeterministic.  So, the authors appear to desire to bring back determinism and locality.  If there were a horse race between Secretariat and Donald Trump’s entry, MDGA, “Make Determinism Great Again”, we expect these authors would be betting heavily on MDGA.  Nothing wrong with that, in our view in the deductive process all solutions are on the table, unless they have already led to contradictions, and we know of no experiment that currently contradicts the authors’ model.

So although we have leveled some criticism regarding this paper, we do feel it is sufficiently novel to meet the published requirements for publication and believe it is a positive development to see it appear in Physical Review A. Additionally, this paper ought to stimulate further work that could potentially be used to predict and discriminate different experimental signatures depending on the existence and type of non-unitary evolution and by using a controlled interaction to emulate the effects of decoherence. We already have indicated several possibilities for additional studies in our Remarks 1. and 2. above.

[1]         J. Preskill, “Preskill’s Notes,” http://theory.caltech.edu/~preskill/ph219/chap3_15.pdf.

[2]         A. K. Rajagopal and R. W. Rendell, “Decoherence, correlation, and entanglement in a pair of coupled quantum dissipative oscillators,” Phys Rev A  (Coll Park), vol. 63, no. 2, p. 22116, Jan. 2001, doi: 10.1103/PhysRevA.63.022116.

[3]         T. Yu and J. H. Eberly, “Sudden Death of Entanglement,” Science (1979), vol. 323, no. 5914, pp. 598–601, Jan. 2009, doi: 10.1126/science.1167343.

[4]         J. R. Hance and S. Hossenfelder, “What does it take to solve the measurement problem?,” J Phys Commun, vol. 6, no. 10, p. 102001, 2022, doi: 10.1088/2399-6528/ac96cf.

[5]         M. Steiner and R. Rendell, The Quantum Measurement Problem. Inspire Institute, 2018.

[6]         Sabine Hossenfelder, “Does Superdeterminism save Quantum Mechanics? Or Does It Kill Free Will and Destroy Science?,” http://backreaction.blogspot.com/2021/12/does-superdeterminism-save-quantum.html, Dec. 18, 2021.

Leave a Reply

Your email address will not be published. Required fields are marked *