Review of Relation between quantum jump and wave function collapse by Tadashi Nakajima, https://doi.org/10.32388/DCB5P3
Summary
A short introduction is given in Sec. I. In Sec. II.A. a synopsis is first given of single-particle measurement theory from a related previous paper by this author. A quantum jump (QJ) is defined as a process of selecting a set of system eigenvalues (SEVs) of an observable. It is proposed that quantum jumps of single-particles occur at the microscopic level (MIJ) and that MIJ are determined from a single measurement. The previous paper [1] did not consider the relationship between QJ and of wave function collapse (WFC), which it the main objective of this paper. The wavefunction is explained to provide a detailed description of the probability distribution of collapse. The author expects that such detailed information of the wavefunction which characterizes a probability distribution cannot collapse except for processes which also allow the characterization of the probability distribution. For single-particle MIJ, he does not believe the wavefunction collapse occurs because a single event cannot provide the probability distribution. After a MIJ occurs, one possible further path is amplification in which the MIP triggers multiplication of secondary particles which eventually produces a macroscopic observable (MAO). Another possible further path is the accumulation of individual MIPs. In this case, the number of MIPs is directly related to the probability distribution. In Secs. B and C examples of amplification of a MIJ is given in terms of photon counting, and an example of accumulation of MIPs is given in a CCD. It appears that Nakajima considers wavefunction collapse only in the case when there is a MAO associated with the probability distribution, hence MIJ does not constitute wavefunction collapse in this author’s theory. In Sec. III many particles are considered. Nakajima claims that a many-particle fermion cannot form a MAO by Pauli’s exclusion principle but that Bosons can. In the former case, according to the author, there is no wavefunction collapse but there can be in the latter case. An exception is the case of Cooper pairs. He goes on to define macroscopic quantum jumps which certain many-particle systems are capable of. The MAO’s are stated to provide a mechanism for wavefunction collapse.
Strengths
- The author considers the possibility of ascribing a physical process at the microscopic level. Many theories and interpretations put forward to explain measurement assume what Nakajima refers to in the previous paper [1] as the Postulate of Classicality of Apparatus (PCA). Essentially that measurement occurs through a macroscopic classical apparatus. On the other hand, the author proposes that measurement can occur at the microscopic level.
- His view appears consistent with Jordan’s viewpoint [2] that there is a real physical process for which measurement occurs: he states in [1]
- However, this MIJ after the selection of the SEVs is a definite physical process such as photoelectric effect. The emission of photoelectron as a MIP is the result of the MIJ. We regard that standard quantum mechanics or the MIJ covers up to the stage of the emission of the MIP.
- Also, he lists processes such as ionization, nucleation, CCD, as measurement processes as well as various amplification processes as measurement processes. Interestingly he also lists in [1] Microwave Kinetic Inductance Detector which utilizes Cooper pairs to provide detection. Note that there are other authors such as Adler that also believe that measurement begins at latent image formation [3]. In fact, one can trace the idea that measurement might occur at the microscopic level to a Solvay conference in 1927 where Born explained that cloud chamber tracks were due to probabilistic measurement [4]
- As soon as such an ionization is shown by the appearance of cloud droplets, in order to describe what happens afterwards one must reduce the wave packet in the immediate vicinity of the drops. One thus obtains a wave packet in the form of a ray, which corresponds to the corpuscular character of the phenomenon of the spherical wave to a wave packet with definite position and momentum.
- Heisenberg also appeared to concur with this explanation. On the other hand, Mott showed that only tracks with straight lines could occur with non-zero probability using Schrödinger’s equation alone [4].
Weaknesses
- Dirac gives the following example of measurement [5, p. 7]
- When we make the photon meet a tourmaline crystal, we are subjecting it to an observation. We are observing whether it is polarized parallel or perpendicular to the optic axis. The effect of making this observation is to force the photon entirely into the state of parallel or entirely into the state of perpendicular polarization. It has to make a sudden jump from being partly in each of these two states to being entirely in one or other of them. Which of the two states it will jump into cannot be predicted, but is governed only by probability laws. Once, the photon is measured, its wavefunction ceases to exist in the process of quantum measurement.
- The author defines “the collapse of wave function to be the measurement of probability distribution from a single measurement.” There is nothing mentioned that we have seen in historical definitions of wave function collapse that requires characterization of the probability distribution, only that the statistics of the measurement obey the distribution. According to Dirac, the energy of the photon will no longer be in the electromagnetic field once a positive measurement occurs such as the case suggested by Dirac that occurs in a tourmaline crystal. In such a case, it can be said according to Dirac that the wavefunction of the photon collapses into the tourmaline crystal.
- Certainly, one can simply ignore the above and define wave function collapse to be the measurement of the probability distribution from a single measurement as the author does. However, this is rather problematic. Suppose as considered by Dirac that a photon is in a superposition with parameter
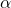 being perpendicular
being perpendicular 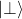 and parallel
and parallel 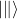 > to the optical axis of tourmaline
> to the optical axis of tourmaline 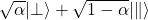 .The probability of being absorbed by the tourmaline is
.The probability of being absorbed by the tourmaline is 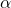 , and this is the statistic that will result in running such an experiment. However, precise knowledge of the actual probability distribution from a single measurement is well-known to be impossible from the no-cloning theorem. One cannot learn the value of
, and this is the statistic that will result in running such an experiment. However, precise knowledge of the actual probability distribution from a single measurement is well-known to be impossible from the no-cloning theorem. One cannot learn the value of 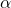 in a single measurement. So, the author’s definition of “wave function collapse” immediately implies it is not a single measurement phenomenon, which is consistent with what he expects. On the other hand, once a measurement occurs and after amplification, one can check that the photon wavefunction does not exist, and this will always be confirmed, including on single measurements. Hence the typical historical definition of wavefunction collapse is that it occurs on each and every positive measurement.
in a single measurement. So, the author’s definition of “wave function collapse” immediately implies it is not a single measurement phenomenon, which is consistent with what he expects. On the other hand, once a measurement occurs and after amplification, one can check that the photon wavefunction does not exist, and this will always be confirmed, including on single measurements. Hence the typical historical definition of wavefunction collapse is that it occurs on each and every positive measurement. - The idea that there is measurement at the microscopic level is something that is proposed by Nakajima in [1], similar to others such as Born in 1927, but no experimental proof or other theory is offered.
Specific Comments
In the reference to Dirac, ”In Paper I, we did not ask the mechanism of the MIJ, since we cannot investigate it by experiments, following the attitude of Dirac”, a reference is given to Dirac’s book, but no page number is included. When one references a specific issue located in a book, one should include the page number the reference refers to with the reference, such as [5, P. 6].
Conclusions
Overall, Nakajima’s original paper [1] is interesting. The discussion in this paper regarding relating wavefunction collapse to measurement seems to be problematic in terms of both the historic development of the theory and also as regards the no-cloning theorem. Lastly, the use of macroscopic quantum objects to perform measurement seems interesting.
One is still left in the dark by Nakajima work as to whether there are a lot of linear tracks in a cloud chamber that exist in a superposition or a single track. One can certainly speculate one way or another, but a much more detailed theory of measurement that predicts the processes which constitute measurement and which is experimentally verified is necessary in order to resolve what we define to be the physical measurement problem in [6].
[1] T. Nakajima, “Microscopic Quantum Jump: An Interpretation of Measurement Problem,” International Journal of Theoretical Physics, vol. 62, no. 3, p. 67, 2023, doi: 10.1007/s10773-023-05326-8.
[2] P. Jordan, “On the process of measurement in quantum mechanics,” Philos Sci, vol. 16, no. 4, 1949.
[3] S. L. Adler, “Connecting the Dots: Mott for Emulsions, Collapse Models, Colored Noise, Frame Dependence of Measurements, Evasion of the ‘Free Will Theorem,’” Found Phys, vol. 48, no. 11, pp. 1557–1567, Nov. 2018, doi: 10.1007/s10701-018-0215-7.
[4] R. Figari and A. Teta, “Emergence of classical trajectories in quantum systems: the cloud chamber problem in the analysis of Mott (1929),” Arch Hist Exact Sci, vol. 67, pp. 215–234, 2012, [Online]. Available: https://api.semanticscholar.org/CorpusID:119665559
[5] P. A. M. Dirac, The Principles of Quantum Mechanics. Clarendon-Press , 1930.
[6] M. Steiner and R. Rendell, The Quantum Measurement Problem. Inspire Institute, 2018.
